Конические сечения и свойства их касательных
Морозов В. В., учитель
математики и информатики МОУ «Школа № 17» г. Полысаево Кемеровской области На рисунке 1 построены прямые этого семейства, где
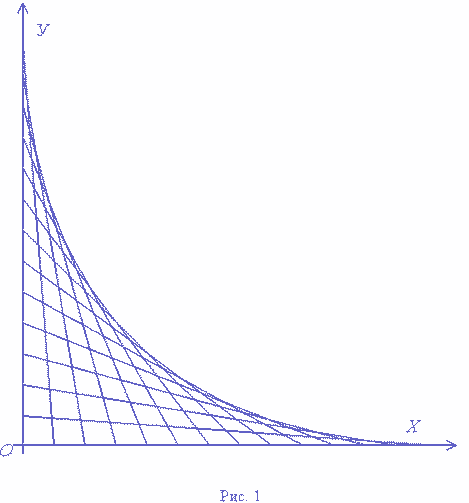 В первой координатной четверти рассмотрим
семейство прямых вида
В первой координатной четверти рассмотрим
семейство прямых вида ![]() , где
, где ![]() ,
, ![]() .
. ![]() с некоторым шагом h. Если шаг h сделать
достаточно малым, то замечаем, что все прямые этого семейства касаются
некоторой кривой линии (рис. 2).
с некоторым шагом h. Если шаг h сделать
достаточно малым, то замечаем, что все прямые этого семейства касаются
некоторой кривой линии (рис. 2).
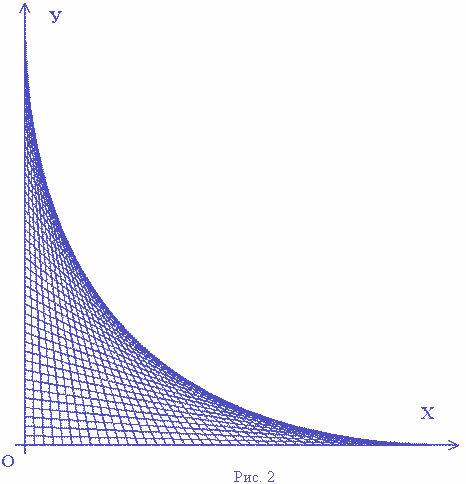
Открываем математическую энциклопедию: «Огибающая семейства линий на плоскости – линия, которая в каждой своей точке касается одной линии семейства».
Что за кривая линия является огибающей нашего семейства прямых? Пытаясь отыскать ответ на этот вопрос, ученица 11 класса Лапицкая Софья выяснила, что огибающая семейства прямых
![]() ;
; ![]() , где
, где ![]() ,
, ![]()
является параболой, ось которой лежит на биссектрисе первой координатной четверти. Более того, им удалось получить некоторые интересные свойства других конических сечений.
Рассмотрим параболу – график функции ![]() , где a>0. Из каких точек плоскости можно провести две различные
касательные к параболе? Очевидно, что из точки M0 можно провести две различных касательных к параболе если и
только если эта точка лежит ниже параболы, то есть координаты точки M0(x0;y0) удовлетворяют условию
, где a>0. Из каких точек плоскости можно провести две различные
касательные к параболе? Очевидно, что из точки M0 можно провести две различных касательных к параболе если и
только если эта точка лежит ниже параболы, то есть координаты точки M0(x0;y0) удовлетворяют условию
![]() .
.
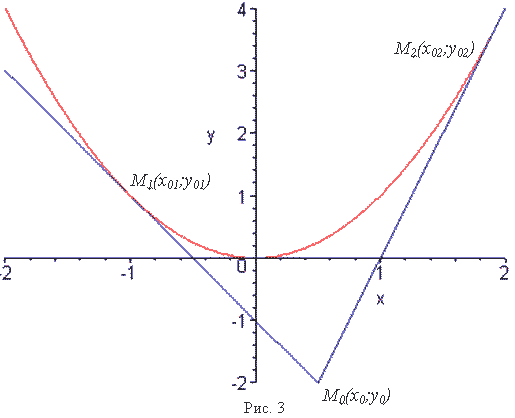 Выберем произвольную точку M0(x0;y0) плоскости, удовлетворяющую этому условию. Проведём через неё
две прямые, касающиеся параболы в точках М1(x01;y01) и
М2(x02;y02) (рис. 3).
Выберем произвольную точку M0(x0;y0) плоскости, удовлетворяющую этому условию. Проведём через неё
две прямые, касающиеся параболы в точках М1(x01;y01) и
М2(x02;y02) (рис. 3).
Выберем на параболе произвольную точку P между M1 и M2. Проведём через неё касательную к параболе. Пусть эта касательная пересекает касательные M0M1 и M0M2 соответственно в точках B1 и B2 (рис. 4).
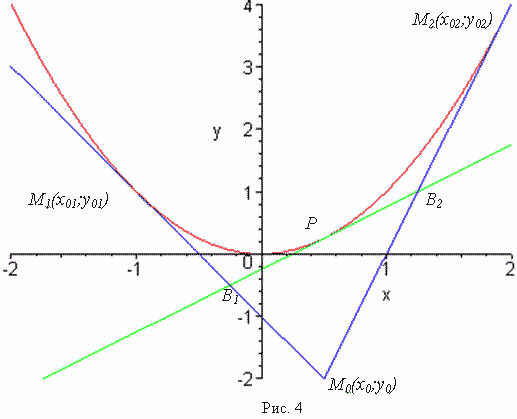 |
Утверждение 1. При выполнении описанных выше условий имеет место
следующее равенство: 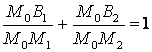 .
.
Сначала докажем лемму о пересечении двух касательных к параболе.
Лемма. Пусть две прямые, касающиеся параболы ![]() в различных точках
в различных точках ![]() и
и ![]() , пересекаются в точке
, пересекаются в точке ![]() . Тогда
. Тогда
![]() ,
, ![]() .
.
Доказательство леммы. Уравнение касательной к параболе ![]() в точке А имеет
вид
в точке А имеет
вид ![]() , а
после упрощения
, а
после упрощения ![]() .
Точно также уравнение касательной к параболе
.
Точно также уравнение касательной к параболе ![]() в точке B
имеет вид
в точке B
имеет вид ![]() . Для
поиска координат точки пересечения касательных решаем систему
. Для
поиска координат точки пересечения касательных решаем систему

![]() ,
,
![]() .
.
Так как ![]() по
условию, то
по
условию, то ![]() .
Тогда
.
Тогда
![]() .
.
Итак, ![]() ,
,
![]() . Лемма
доказана.
. Лемма
доказана.
Доказательство утверждения 1. Пусть прямые, касающиеся параболы в точках М1(x01;y01) и М2(x02;y02) пересекаются в точке M0(x0;y0). Тогда по доказанной выше лемме координаты этих трёх точек связаны соотношениями
![]() ,
, ![]() .
.
Найдём квадраты расстояний от М0 до М1 и до М2.
![]() .
.
![]() .
.
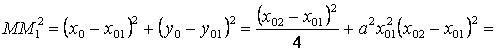
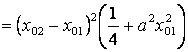 .
.
Аналогично, 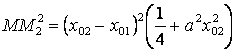 .
.
Через произвольную точку P(p,ap2) на параболе ![]() между точками M1 и M2 проведём
касательную, которая пересекает касательные M0M1 и M0M2 соответственно в точках B1 и B2 (рис. 4). По
доказанной выше лемме получаем координаты точек B1 и B2.
между точками M1 и M2 проведём
касательную, которая пересекает касательные M0M1 и M0M2 соответственно в точках B1 и B2 (рис. 4). По
доказанной выше лемме получаем координаты точек B1 и B2.
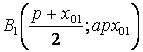 ,
, 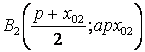 .
.
Найдём квадраты расстояний от М0 до B1 и до B2.
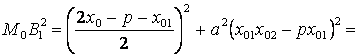
 .
.
Аналогично, 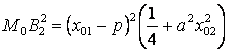 . Тогда
. Тогда
 ,
, 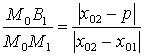 .
.
Точно также  .
Тогда
.
Тогда
 .
.
Так как точка P на параболе лежит между
точками M1 и M2, то ![]() , поэтому
, поэтому 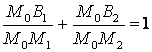 .
.
Утверждение 1 доказано.
Верно и обратное утверждение. Пусть прямые, касающиеся параболы ![]() в точках M1 и M2 пересекаются в точке M0.
Пусть на отрезках M0M1 и M0M2 выбраны точки B1 и B2 соответственно так, что
в точках M1 и M2 пересекаются в точке M0.
Пусть на отрезках M0M1 и M0M2 выбраны точки B1 и B2 соответственно так, что 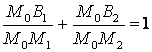 . Тогда прямая B1B2
касается этой параболы.
. Тогда прямая B1B2
касается этой параболы.
Действительно, если допустить противное, то на параболе между точками M1 и M2 существует точка P, в которой касательная параллельна B1B2.
Пусть эта касательная пересекает касательные M0M1 и M0M2 соответственно в точках С1 и С2. Тогда
по утверждению 1  .
Причём, в силу подобия треугольников M0B1B2
и M0С1С2 либо
одновременно
.
Причём, в силу подобия треугольников M0B1B2
и M0С1С2 либо
одновременно 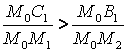 и
и
 , Либо
одновременно
, Либо
одновременно 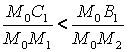 и
и
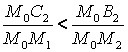 , А,
следовательно,
, А,
следовательно,  .
Полученное противоречие доказывает обратное утверждение.
.
Полученное противоречие доказывает обратное утверждение.
Замечание. Нетрудно видеть, что в утверждении 1 можно позволить
точке P быть на параболе
не только между точками M1 и M2. Если точка P левее точки M1, то  .
.
Если точка P правее точки M2,
то 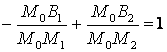 .
.
Следствие 1. Если точка М0 лежит на оси ординат,
то ![]() (рис.
5).
(рис.
5).
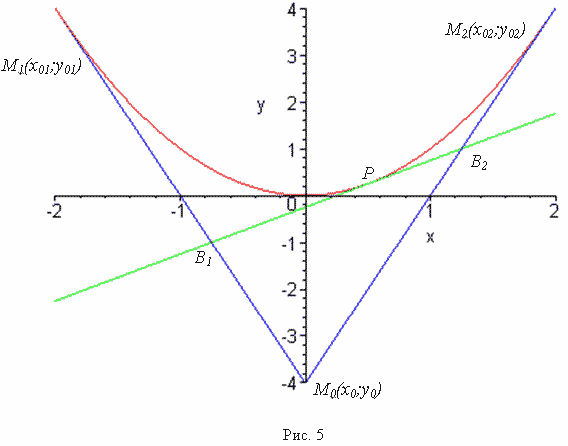 |
Иными словами, если ![]() , то
, то ![]() .
.
Вернёмся к нашему первому примеру. Если в первую координатную четверть
вписана парабола, касающаяся осей ОХ и ОY в точках ![]() и
и ![]() ,
, ![]() , и если прямая
, и если прямая ![]() касается параболы, то согласно
утверждению 1
касается параболы, то согласно
утверждению 1 ![]() .
Таким образом, мы получили…
.
Таким образом, мы получили…
Следствие 2. Огибающей семейства прямых ![]() , где
, где ![]() является парабола.
является парабола.
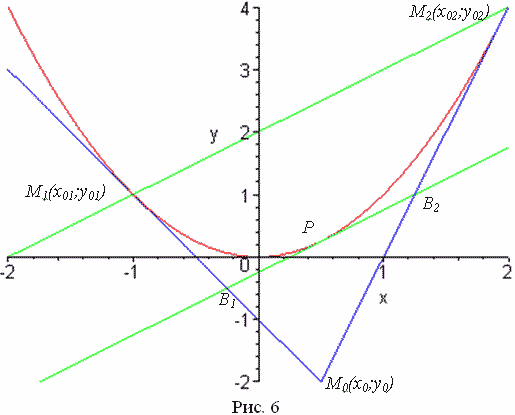 Следствие 3. Пусть прямые,
касающиеся параболы в точках M1 и M2 пересекаются
в точке M0. Тогда средняя линия
треугольника M1M2M0,
параллельная M1M2,
касается параболы (рис. 6).
Следствие 3. Пусть прямые,
касающиеся параболы в точках M1 и M2 пересекаются
в точке M0. Тогда средняя линия
треугольника M1M2M0,
параллельная M1M2,
касается параболы (рис. 6).
Действительно, пусть B1B2
– средняя линия треугольника M1M2M0.
Тогда  . Следовательно
B1B2 касается параболы.
. Следовательно
B1B2 касается параболы.
Далее, нетрудно убедиться, что уравнение прямой B1B2 имеет вид
![]() .
.
Найдём координаты точки касания прямой B1B2 и параболы, решая систему

![]()
![]() .
.
Разумеется, последнее уравнение имеет единственное решение, а поэтому абсцисса Р точки касания (см. рис. 6) та же, что и у точки М0, а поэтому прямая М0Р всегда параллельна оси ординат.
Теперь легко получаем координаты не только точек B1 и B2, но и точки касания Р:
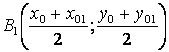 ,
, 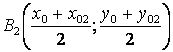 ,
, ![]() .
.
Нетрудно убедиться, что абсцисса точки Р равна среднему арифметическому абсцисс точек B1 и B2. Убедимся также, что ордината точки Р равна среднему арифметическому ординат точек B1 и B2. Действительно, используя лемму, получаем.
![]()
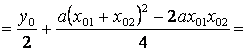
![]() .
.
Таким образом, мы получили…
Следствие 4. Пусть прямые, касающиеся параболы в точках M1 и M2 пересекаются в точке M0. Тогда средняя линия B1B2 треугольника M1M2M0, параллельная M1M2, касается параболы в точке P – середине средней линии B1B2, причём прямая М0Р является медианой треугольника M1M2M0 и параллельна оси ординат (рис. 7).
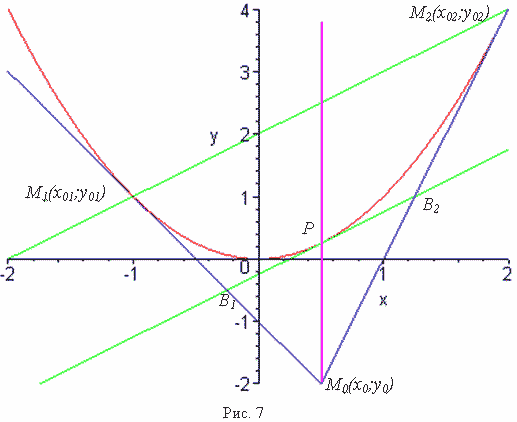 |
Следствие 5. В данный неразвёрнутый угол можно вписать единственную параболу, касающуюся сторон угла в двух данных (отличных от вершины) точках.
Действительно, пусть дан угол с вершиной М0 и точки M1 и M2 на сторонах угла. У треугольника M1M2M0 построим среднюю линию и отметим её середину Р. Для треугольников M1B1P и M2B2P проделаем то же самое. Этот процесс продолжаем бесконечно. К семейству полученных средних линий добавим ещё пару сторон данного угла. Это семейство – семейство огибающих дуги параболы, касающейся сторон угла в двух данных точках. Единственность параболы вытекает из известного утверждения, что через три точки плоскости, не лежащие на одной прямой проходит единственная парабола. Заодно мы получили интересный способ построения параболы.
Итак, мы рассмотрели свойство касательных к параболе и получили семейство прямых, огибающей которых является парабола. Возникает вопрос: можно ли доказать похожие свойства для других конических сечений: гиперболы, эллипса, окружности?
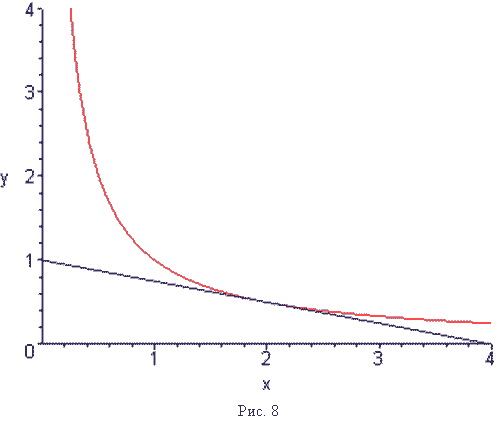 В первой координатной четверти рассмотрим
гиперболу
В первой координатной четверти рассмотрим
гиперболу ![]() .
Построим касательную к гиперболе в некоторой точке
.
Построим касательную к гиперболе в некоторой точке ![]() и найдём длины отрезков,
отсекаемых касательной от осей координат (рис. 8).
и найдём длины отрезков,
отсекаемых касательной от осей координат (рис. 8).
Уравнение касательной к гиперболе ![]() имеет вид
имеет вид 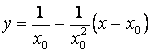 , а после упрощения
, а после упрощения 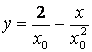 . Тогда длины отрезков,
отсекаемых касательной от асимптот гиперболы равны
. Тогда длины отрезков,
отсекаемых касательной от асимптот гиперболы равны ![]() и
и ![]() . Замечаем, что произведение длин этих
отрезков не зависит от выбора точки касания:
. Замечаем, что произведение длин этих
отрезков не зависит от выбора точки касания:  .
.
Таким образом, огибающей семейства прямых ![]() , где
, где ![]() ,
, ![]() является гипербола, уравнение которой
является гипербола, уравнение которой ![]() .
.
Можно получить общий результат о касательных к гиперболе.
Утверждение 2. Касательная к гиперболе в произвольной точке отсекает от асимптот отрезки, произведение которых постоянно и не зависит от выбора точки касания.
Доказательство. Рассмотрим гиперболу 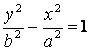 . Асимптоты этой гиперболы – прямые
. Асимптоты этой гиперболы – прямые ![]() . Получим уравнение
верхней ветви гиперболы:
. Получим уравнение
верхней ветви гиперболы:
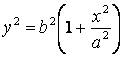 ,
,  ,
, ![]() .
.
Найдём уравнение касательной к верхней ветви гиперболы.
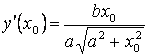 ,
, ![]() .
.
Уравнение касательной имеет вид
 .
.
 Найдём координаты абсциссы точек
пересечения касательной к гиперболе и её асимптотами
Найдём координаты абсциссы точек
пересечения касательной к гиперболе и её асимптотами ![]() (рис. 9).
(рис. 9).
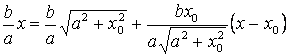 ,
,
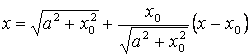 ,
,
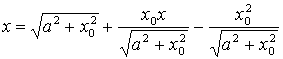 ,
,
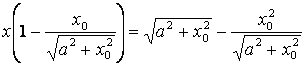 ,
,
 ,
,
 .
.
Так как ![]() ,
то
,
то 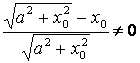 и
и
 ,
,
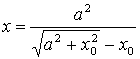 .
.
Координаты точки ![]() пересечения касательной к гиперболе и
асимптоты:
пересечения касательной к гиперболе и
асимптоты:
 ,
, 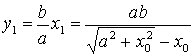 ;
;
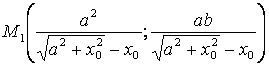 .
.
Точно также получаем координаты точки M2.
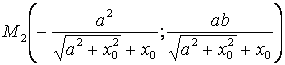 .
.
Тогда
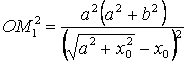 ;
; 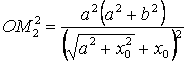 .
.
И, наконец, получаем:
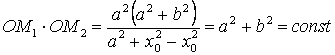 .
.
Утверждение 2 доказано.
Таким образом, для гиперболы площадь треугольника, ограниченного асимптотами и касательной постоянна.
Для окружности аналогичное свойство получить и вовсе просто. Из точки М проведём пару прямых, касающихся окружности в точках А и В, которые разбивают окружность на две дуги. На меньшей из этих дуг выберем произвольную точку Е и проведём через неё касательную, которая пересекает касательные МА и МВ в точках С и D соответственно (рис. 10).
 |
Утверждение 3. Периметр треугольника MCD постоянен и не зависит от выбора точки касания Е.
Действительно, легко видеть, что СА=CE, DB=DE, поэтому периметр треугольника MCD равен
![]()
![]() . Утверждение
доказано.
. Утверждение
доказано.
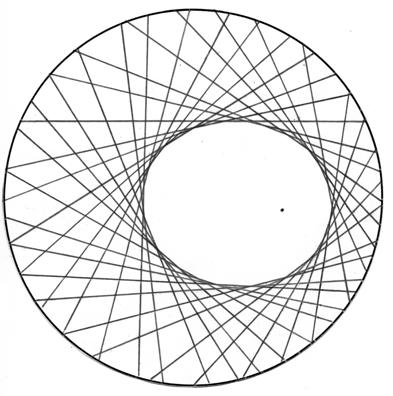 Касательные к эллипсу, другому
коническому сечению, также обладают интересным свойством. Вырежем из бумаги
большой круг и в любом его месте, поставим точку. Сложим круг так, чтобы эта
точка оказалась под любой точкой окружности на краю диска. Разогнём листок и
снова согнём, прикрыв точку уже другим местом на окружности. Сделаем так
несколько раз, пока вся бумага не покроется сгибами, которые образуют семейство
касательных к эллипсу (рис 11).
Касательные к эллипсу, другому
коническому сечению, также обладают интересным свойством. Вырежем из бумаги
большой круг и в любом его месте, поставим точку. Сложим круг так, чтобы эта
точка оказалась под любой точкой окружности на краю диска. Разогнём листок и
снова согнём, прикрыв точку уже другим местом на окружности. Сделаем так
несколько раз, пока вся бумага не покроется сгибами, которые образуют семейство
касательных к эллипсу (рис 11).
Рис. 11
Утверждение 4. Каждая линия сгиба при описанной выше процедуре касается эллипса с фокусами в выбранной точке Р и центре окружности О.
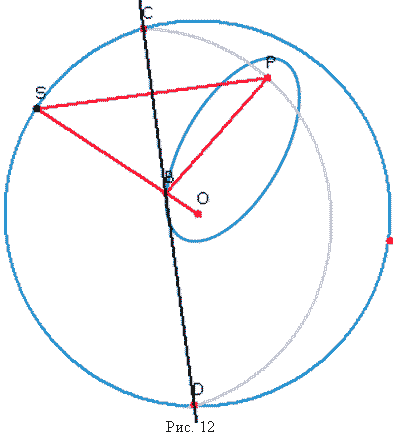 |
Доказательство. Пусть точка P – любая точка круга, не являющаяся его центром О (рис. 12). Мы сгибаем круг так, чтобы совместить точку P с какой-нибудь точкой окружности S. При этом линией сгиба должна быть прямая DB, которая перпендикулярна PS и делит отрезок PS пополам. Отсюда следует, что BS и BP равны, а поэтому ОB+BP=ОB+ВS постоянно и равно радиусу окружности. Отрезок ОB+BS представляет собой сумму расстояний от точки B до фиксированных точек P и О, поэтому геометрическим местом точек B (движущихся при перемещении точки S по окружности) является эллипс с фокусами в точках P и О.
Линия сгиба DC является касательной к эллипсу в точке B, потому что она образует равные углы с прямыми, проведенными из фокусов в точку B, поскольку угол PBC равен углу SBC, который в свою очередь равен углу OBD. Линии сгиба всегда касаются эллипса, поэтому эллипс является огибающей семейства линий сгиба. Утверждение доказано.
Нетрудно убедиться, что большая ось полученного таким способом эллипса равна радиусу данной окружности.
Утверждение 5. Точка пересечения высот остроугольного треугольника является фокусом вписанного в этот треугольник эллипса.
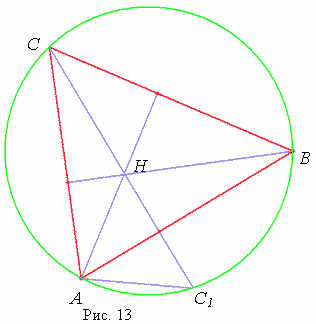 Лемма. Точки, симметричные точке
пересечения высот треугольника относительно его сторон, лежат на
описанной около этого треугольника окружности (рис. 13).
Лемма. Точки, симметричные точке
пересечения высот треугольника относительно его сторон, лежат на
описанной около этого треугольника окружности (рис. 13).
Доказательство леммы. Пусть A1, B1 и C1 – точки, симметричные точке пересечения высот треугольника H относительно сторон BC, CA и AB соответственно. Так как AB^CH и BC^AH, то углы межу прямыми AB и BC и угол между прямыми CH и HA равны. ÐABC=ÐC1HA, а так как треугольник AC1H равнобедренный, то ÐC1HA = ÐAC1C. Следовательно, ÐABC = ÐAC1C, опираются эти углы на одну и туже дугу АС. Значит, точка C1 лежит на описанной окружности треугольника ABC. Аналогично доказывается, что точки A1 и B1 лежат на этой окружности. Лемма доказана.
Следствие. Образы окружности при осевой симметрии относительно сторон вписанного в эту окружность треугольника пересекаются в точке пересечения высот треугольника.
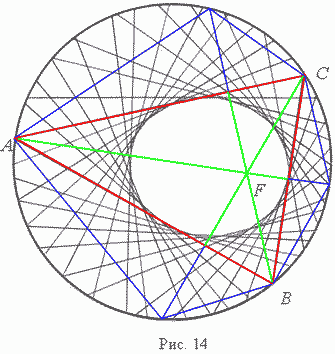 Иными словами, если перегнуть круг по
сторонам вписанного треугольника, то все три получившиеся дуги пересекаются в
одной точке – точке пересечения высот треугольника.
Иными словами, если перегнуть круг по
сторонам вписанного треугольника, то все три получившиеся дуги пересекаются в
одной точке – точке пересечения высот треугольника.
Теперь докажем утверждение 5.
Пусть дан эллипс, обозначим его фокусы О и F. Строим окружность с центром в одном из его фокусов О радиусом, равным его большой полуоси. Таким образом, эта окружность обладает следующим свойством: если перегнуть полученный таким образом круг по касательной к эллипсу, то точка окружности попадает на фокус F.
Из любой точки A на окружности строим 2 касательных к эллипсу. По построению при перегибе круга по этим касательным точки на окружности попадает на фокус F. Эти касательные пересекают окружность в двух других точках B и C, однозначно определяя треугольник ABC, вписанный в окружность (рис. 14).
Как доказано выше, точка F пересечения высот этого треугольника также переходит на окружность.
Но эта же точка F – переходит на окружность при симметрии относительно третьей стороны. Следовательно, третья сторона треугольника – касается эллипса.
Таким образом, точка пересечения высот треугольника является фокусом некоторого вписанного в этот треугольник эллипса. Утверждение доказано.
Теорема Эйлера. Во всяком треугольнике точка пересечения медиан, точка пересечения высот (или их продолжений) и точка пересечения серединных перпендикуляров к сторонам треугольника лежат на одной прямой, которая называется прямой Эйлера.
Таким образом, прямая Эйлера остроугольного треугольника является осью симметрии вписанного в этот треугольник эллипса, и точка пересечения медиан треугольника также лежит на оси вписанного в треугольник эллипса.
Кстати, известно, что радиус окружности Эйлера (она известна ещё как окружность 9 точек) равен половине радиуса описанной окружности, а центр окружности Эйлера является серединой отрезка, соединяющего ортоцентр с центром описанной окружности. Таким образом, центр нашего эллипса (середина отрезка между фокусами) является центром окружности Эйлера, в которую вписан эллипс.
Во всех полученных утверждениях усматривается нечто общее:
- для параболы постоянна сумма боковых сторон треугольника, ограниченного тремя касательными, две из которых проведены из точки на оси параболы (рис. 5);
- для гиперболы постоянна площадь треугольника, ограниченного асимптотами и касательной (рис. 9);
- для окружности постоянен периметр треугольника, ограниченного касательными (рис. 10);
- эллипс является огибающей семейства треугольников, вписанных в одну и ту же окружность с центром в одном фокусе эллипса, а точки пересечения высот каждого из этих треугольников – второй фокус эллипса, центр этого эллипса – центр окружности Эйлера каждого из этих треугольников; у каждого из этих треугольников одни и те же прямая Эйлера и окружность Эйлера (рис. 14).
В заключении работы в качестве иллюстрации описанных здесь явлений мы предоставляем читателю скачать программы и их исходные коды.